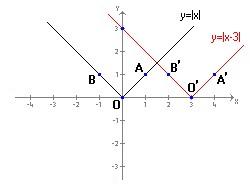
O(0,0)
![]() O′(3,0)
O′(3,0)
A(1,1)
![]() A′(4,1)
A′(4,1)
B(-1,1)
![]() B′(2,1)
B′(2,1)
| didattica on line > materiali didattici > matematica > unità didattiche > Unità 4 (Testo dell'Unità) |
| pagina aggiornata il 02/06/2003 |
|
unità 4 - Traslazioni / Testo dell'Unità |
Corso di Matematica - Traslazioni (Pagina 4 di 6)
| Vai alle Traslazioni Verticali | Vai alle Traslazioni Oblique | |
|
TRASLAZIONI ORIZZONTALI |
||
|
(4 di 4) |
||
Possiamo quindi generalizzare: y=|x+a| con a costante reale ha un grafico che rispetto a quello di y=|x| risulta traslato orizzontalmente verso destra se a<0 o verso sinistra se a>0.
In entrambi i casi la traslazione è di |a| ; infatti la costante a rappresenta un numero relativo e il suo segno indica se la traslazione avviene verso sinistra o verso destra, mentre il suo valore assoluto indica di quanto il grafico è traslato rispetto a quello “standard” y=|x|.
Osserviamo anche che la funzione y=|x+a| è ottenuta da y=|x| tramite una sostituzione: x+a al posto di x.
- - -
Se siamo in grado di capire la traslazione associata alla funzione y=|x+a| possiamo anche ottenere il suo grafico da quello di y=|x| traslando tre punti opportuni: l’origine e un punto su ciascuna delle due semirette componenti il grafico
|
O(0,0)
A(1,1)
B(-1,1)
|
|
|
Unità 4 - Pagina 4 di 6 |
|
|
|
copyright © 2003 IISS Des Ambrois - Oulx (TO) Italia |
||
|
Tutti i diritti riservati |
||