Corso di Matematica - Traslazioni (Pagina 5 di 6)

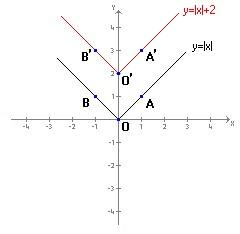
Consideriamo la funzione y=|x|+2.

Siccome si può anche scrivere y-2=|x| si vede che è ottenuta da y=|x| sostituendo y-2 al posto di y.

A cosa corrisponde tale sostituzione?

Essendo la y uguale a |x|+2 , i punti del grafico a parità di ascissa x avranno un’ordinata y ottenuta aggiungendo 2 a |x|, ossia si troveranno “più in alto di 2 unità rispetto ai punti di y=|x|. Quindi il grafico di y=|x|+2 può essere ottenuto da quello di y=|x| mediante una traslazione verticale verso l’alto di 2.

Se volessimo tracciare il grafico ad esempio di y=|x|-3 potremmo traslare il grafico di y=|x| verso il basso di 3

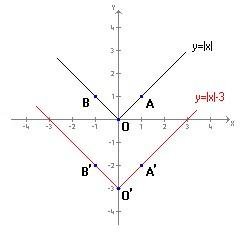
Possiamo quindi generalizzare: il grafico di y=|x|+a rispetto a quello di y=|x| risulta traslato verticalmente verso l’alto se a>0, verso il basso se a<0.

Attenzione: a non rappresenta di per sé un valore positivo, come –a non rappresenta necessariamente un valore negativo per il fatto che compare il segno “-“ ; a è un numero relativo e quindi possiede un segno. Se a>0 allora –a<0, ma se a<0 allora –a>0.

	Unità 4 - Pagina 5 di 6
copyright © 2003 IISS Des Ambrois - Oulx (TO) Italia
desambro@tin.it
Tutti i diritti riservati