| didattica on line > materiali didattici > matematica > unità didattiche > Unità 4 (Testo dell'Unità) |
| pagina aggiornata il 02/06/2003 |
|
unità 4 - Traslazioni / Testo dell'Unità |
Liceo - Indirizzi Classico, Linguistico, Scientifico
Corso di Matematica - Traslazioni
| Vai alle Traslazioni Verticali | Vai alle Traslazioni Oblique | |
|
TRASLAZIONI ORIZZONTALI |
||
|
(1 di 4) |
||
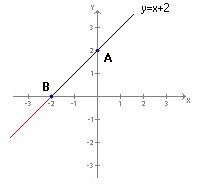
Consideriamo la funzione y=|x+2| ottenuta dalla funzione modulo “standard” y=|x| sostituendo x+2 al posto di x.
A cosa corrisponde tale sostituzione?
Disegniamo il grafico di y=x+2 aiutandoci con la tabella
|
x |
y |
|
0 |
0+2=2 |
|
-2 |
-2+2=0 |
Attenzione: conviene scegliere come valori di x:
| (1) | 0 perché così si trova il punto A(0,2) della che sta sull’asse y |
| (2) | il valore di x che rende nullo, ossia uguale a o, il corrispondente valore di y (nel nostro caso tale valore di x è -2 perché sostituito in y=x+2 si ottiene y=-2+2=0) così si trova il punto B(-2,0) della retta che sta sull’asse x |
Congiungendo i punti A e B si ottiene il grafico della retta.

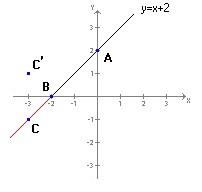
Poi si “ribalta” al di sopra dell’asse x la parte di grafico situata al di sotto dell’asse x (parte disegnata in rosso); per fare questo si sceglie un punto C della retta che stia su questa semiretta: C avrà una ascissa minore di -2, ad esempio -3.
|
x |
y |
|
-3 |
-3+2=-1 |
C(-3,-1)
Se ribaltiamo C al di sopra dell’asse x troviamo C′, simmetrico di C rispetto all’asse x, che ha la stessa ascissa di C ma ordinata opposta
C(-3,-1)
![]() C′(-3,+1)
C′(-3,+1)
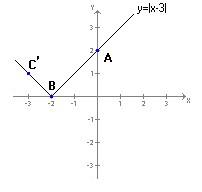
e congiungendo B con C′ si ottiene la semiretta che completa il grafico di y=|x+2|
|
|
Unità 4 - Pagina 1 di 6 |
|
|
copyright © 2003 IISS Des Ambrois - Oulx (TO) Italia |
||
|
Tutti i diritti riservati |
||