Corso di Matematica - Simmetrie (Pagina 3 di 5)

Consideriamo un punto P sul piano cartesiano ed il suo simmetrico P' rispetto all’asse y; vogliamo capire la relazione tra le loro coordinate.

Supponiamo ad esempio che P abbia coordinate (2,3). Allora la distanza di P dall’asse y sarà uguale alla distanza di P' dall’asse, e il segmento PP' sarà perpendicolare all’asse y. P' risulta avere coordinate (-2,3).

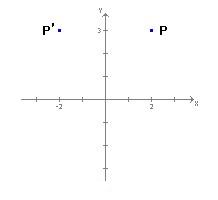
In generale una simmetria rispetto all’asse y è una trasformazione che ad ogni punto P(x,y) associa un punto P'(-x,y) avente stessa ordinata di P e ascissa opposta.

Possiamo applicare la simmetria ad un grafico anziché ad un singolo punto; per trovare il grafico simmetrico basterà scegliere opportunamente alcuni punti del grafico dato, trovare i loro trasformati mediante la simmetria e tracciare quindi il grafico passante per essi.

- - -

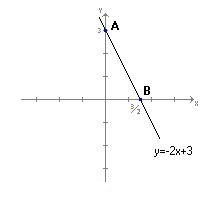
Consideriamo ad esempio la retta di equazione y=-2x+3. Innanzi tutto la  rappresentiamo nel piano congiungendo due punti trovati con l’aiuto di una tabella

dove i valori di x sono scelti arbitrariamente, come più ci fa comodo, mentre i corrispondenti valori di y vengono trovati sostituendo i valori di x nell’espressione  “-2x+3”; si fa anche notare che come valori di x sono stati scelti lo 0 perché così si ottiene il punto della retta situato sull’asse y, e 3/2 perché così si ottiene il punto della retta situato sull’asse x.

Abbiamo così individuato i punti A(0,3) e B(3/2,0), e possiamo tracciare il grafico della retta

Troviamo poi i punti A' e B' simmetrici di A e B rispetto all’asse y: saranno A'(0,3) e B'(-3/2,0).

Congiungendo tali punti si trova il grafico della retta simmetrica di quella data rispetto all’asse x

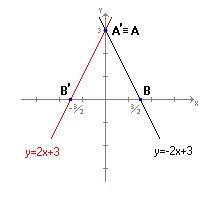
Si può notare che il punto A' coincide con A, e le due rette passano entrambe per questo punto comune. Non si tratta di un caso: infatti A appartiene proprio all’asse y che è l’asse di simmetria, e ogni punto dell’asse di simmetria ha il simmetrico coincidente con se stesso. D’altra parte l’ascissa di tali punti è 0, e l’opposto di 0 è ancora 0!

I punti che hanno la caratteristica di coincidere con il proprio trasformato si dicono punti fissi o uniti.

Allora adesso risulterà chiaro che per trovare il grafico simmetrico conviene individuare l’intersezione della retta data con l’asse y, dato che si tratta di un punto fisso.

Per il momento abbiamo trovato il grafico simmetrico a quello della retta data di equazione y=-2x+3. Ma qual è l’equazione della retta così ottenuta? Per trovarla basta cambiare segno alla x nell’equazione di partenza, perché questo è l’effetto di una simmetria rispetto all’asse y. Dunque si ha: y=-2(-x)+3 e quindi y=2x+3.

Si potrebbe provare a disegnare questa retta congiungendo due suoi punti individuati tramite una tabella, e verificare che si ottiene proprio la retta ottenuta precedentemente per simmetria.

	Unità 5 - Pagina 3 di 5
copyright © 2003 IISS Des Ambrois - Oulx (TO) Italia
desambro@tin.it
Tutti i diritti riservati